좀 빠르게 돌아왔습니다. 이제 일주일에 2번 정도 업로드 목표로 열심히 해보겠습니다! 바로 시작하겠습니다!
이 C language에는 여러가지에 형(type)이 존재합니다. 예를들면 int, char, float, double등이 존재하죠.
그런데 이게 코드를 짜다보면 형이 다른 변수 끼리 대입을 해야하는 연산이 필요로 할 때가 있습니다. 예를 들면 double형 변수의 값을 int형에 대입시키는 등에 경우가 있을 수 있습니다.
하지만 이놈의 C놈은(언어) 형이 다른 변수 끼리의 대입이나 연산들이 모두 불법입니다.
우선 예시를 한번 보시죠 figure.1입니다.

성공적으로 컴파일 한다면 결과는 2가 나올 것입니다.
하지만 에러가 없이 출력되었다고 해서 아무일도 없는것은 아니죠. 아마도 Output에 다음과 같은 메시지가 출력되셨을 겁니다.


저자께서 친절하게 번역까지 해주셨습니다.
이것은 컴파일러 경고(Warning) 메세지로서, 컴퓨터가 우리 유저가 형에 맞지 않게 값을 대입했고, 이로인해 데이터 손실이 발생할 수 있다고 얘기 해줍니다(큐트 컴퓨터)
데이터 손실이 어디서 발생하였는지는 다들 아실 겁니다. 원래는 -2가 나와야 정확하지만 a는 int형이기에 정수만 출력이 됩니다.
그렇다면 컴퓨터는 실수를 어떻게 표현할까요??
사전경고!!!!!!!!!!!!!!!!!!!이해 안되시면 그냥 오늘꺼는 앞 부분만 읽으셔도 됩니다(진짜 뒤로가기 한다고?)

자 설명을 같이 이해해보죠. 컴퓨터는 이진수로 모든 데이터를 표현하는 이진수 바라기 입니다. 과연 이진수 바라기는 어떤식으로 실수를 표현할까요?
C언어에서는 실수를 보관하는 데이터 형을 float과 double로 처리합니다. 컴퓨터 상에서 실수를 표현하는 방법은 대표적으로 2가지
고정 소수점(Fixed Point)와 부동 소수점(Floating Point) 방식입니다. float이 어디서 왔는지는 유추가 되시죠?
우리가 사용하는 컴퓨터의 아마 대부분은 부동 소수점 방식을 통해 실수를 표현 할 것입니다. 그 이유는 고정 소수점에 비해 같은 수의 비트만 사용해서 표현할 수 있는 수의 범위가 더 넓기 때문입니다.
이 방식은 IEEE 754라는 표준을 기반으로 합니다. 이는 IEEE라는 국제전기전자기술자협회에서 1985년에 표준화 된것입니다.
일반적으로 우리가 수를 표현하는 방법은 다음과 같습니다.
123.1234.123. -234 이러한 수 표기를 과학적 표기(scientific notation)으로 표기하면 다음과 같습니다(왜 이렇게 어려운지는 저도 잘 모릅니다 ㅡㅡ)

위 방식이 컴퓨터 상에서 실수를 표현하는 아주 중요한 기법입니다.
마찬가지로 컴퓨터 상에서 소수는 다음과 같이 표현합니다.

이때 f는 ㄱ가수, b는 밑, e는 지수입니다. 예를 들어 123의 경우 f는 1.23, b는 10, e는 2가 됩니다.
컴퓨터는 이진수 바라기라서 b의값은 2로 고정이 됩니다. 그래서 f와e값만 저장하면 됩니다. 마지막으로 맨 앞 부호 비트를 위해 1비트를 더 쓰게 됩니다. 양수면 0 음수면 1이 됩니다.
아래 figure.2은 IEEE 754에서 정의한 부동 소수점 표현 입니다(이제 수를 혐오하시는 분들은 뒤로가기 누르세요 경고했습니다)

float의 경우 가수 부분이 23bit를 차지하고, 지수 부분이 8bit, 그리고 부호 비트가 1bit를 차지하여 총 4byte를 차지합니다.
double의 경우는 가수 부분이 52bit고 지수 부분이 11bit로 무려 8byte를 차지하는 거대한 자료형입니다.
자 마지막으로 소수의 10진법 - 2진법 진법 변환에 대해서 알아보고 마치겠습니다(제가 수를 그만 보고 싶네요 그만 그만!!!!)
10010.1011(2)를 십진법으로 바꿔보는 연습을 해봅시다.
소수점 이하 부분은 마찬가지로 자리수 마다 2의-1승, 2의-2승 순으로 내려갑니다. 십진법에서 10의-1승 순으로 내려가는 것과 동일하죠 따라서 다음과 같습니다.

반대로 십진법 소수를 2진법으로 바꿔볼까요? 대상은 -118.625입니다.
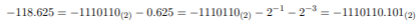
위와 같은 방법으로 십진법 소수를 2진법으로 바꿀 수 있습니다. 안타까운 사실은(숫자만 보여줘서 벌받은거임) 십진법으로 표현된 수를 모두 2진법으로 변환할 수는 없습니다. 예를 들어 0.1의 경우 아래와 같이 무한 소수로 나타나게 됩니다.

이는 무한 등비수열의 합을 구하는 방법을 안다면(아시는분 댓글좀) 0.1이 바뀐 무한 이진 소수가 참임을 알수있다(그만하자 닝겐)

(이렇대~)
컴퓨터는 이처럼 무한히 길게 나타나는 무한 소수들을 모두 나타낼 수 없기에 일정 부분만 잘라 메모리에 보관합니다. 따라서 오차가 발생할 수 밖에 없습니다.
(내용이 매우 길어서 2개로 나누어 형 변환에 대해 올리겠습니다! 고생하셨습니다! 수학은 그만 하고 싶네요 ㅡㅡ )
'C language(c언어)' 카테고리의 다른 글
| 배열(Array)에 대해 알아보자! (0) | 2024.10.01 |
|---|---|
| 형 변환(타입 캐스팅) IEEE754 -2 (돌아왔구나 c식아) (2) | 2024.09.30 |
| Switch문 (2) | 2024.01.29 |
| Loop 반복문 (while문) (do-while문) (0) | 2023.11.03 |
| Loop 반복문 (break) (continue) (0) | 2023.09.11 |